Text Generator ᐈ #1【ℭ𝔬𝔭𝔶 Ⓐⓝⓓ ℙ𝕒𝕤𝕥𝕖】✅ Text Font
Text Generator - Generate ℭ𝔬𝔬𝔩 and ⓢⓣⓨⓛⓘⓢⓗ fancy text font with ✌symbols and text emojis, emojis and its 💯% FREE easy copy & paste.

Welcome on the one of the best, text generator website here you can convert your normal text into and stylish looking cool and awesome different types of Unicode text. Which you can copy and easily paste where ever you want it. It does not matter where you want to, this is one of the best text generator website.
Can i use this Text Generator on online gaming platform? like PUBG and Free Fire
Of course you can use our text generator website to generate different different types of username with different different type of stylish text whether its pubg or free fire you can you use in both of them, that's going to make your profile name or avatar name more attractive and more appealing.
Here is the list of some gaming names which has been generated using your text generator website, please see the result.
¤¸¸.•´¯`•¸¸.•..>> ムムᄊ乇尺 刀ムᄊ乇 <<..•.¸¸•´¯`•.¸¸¤
••¤(`×[¤ ɠąɱɛཞ ŋąɱɛ ¤]×´)¤••
•]••´º´•» ₲₳₥ɆⱤ ₦₳₥Ɇ «•´º´••[•
¸„.-•~¹°”ˆ˜¨ ງค๓ēr ຖค๓ē ¨˜ˆ”°¹~•-.„¸
⎝⎝✧GͥOͣDͫ✧⎠⎠ 𝔾𝕒𝕞𝕖𝕣 ℕ𝕒𝕞𝕖 ⎝⎝✧GͥOͣDͫ✧⎠⎠
꧁𓊈𒆜 𝓖𝓪𝓶𝓮𝓻 𝓝𝓪𝓶𝓮 𒆜𓊉꧂
▁ ▂ ▄ ▅ ▆ ▇ █ ɢǟʍɛʀ ռǟʍɛ █ ▇ ▆ ▅ ▄ ▂ ▁
꧁༒༻☬ད ﻮค๓єг ภค๓є ཌ☬༺༒꧂
Text Generator Guru is a Font Generator Website which helps to Create Cool Text & Cool Fonts for Social Media Websites. Impress your friends with Fancy Fonts and Fancy Text by Simply Type, Copy & Paste on https://textgeneratorguru.com/ If you are looking for a Text Generator Website to create your Font into a Cool Texts or Fancy Texts to write your Status or Send Messages on Social Media Platforms like Facebook, Twitter, Instagram etc, Then why to wait just enter you Text on https://textgeneratorguru.com/ and it’s done. This Website is 100% Free and has huge selections of easy to use Copy & Paste Fonts & Text to turn your Bio into an attractive noticeable & Stand out from the Crowd.
How to Use this Text Fonts Generator Websites?
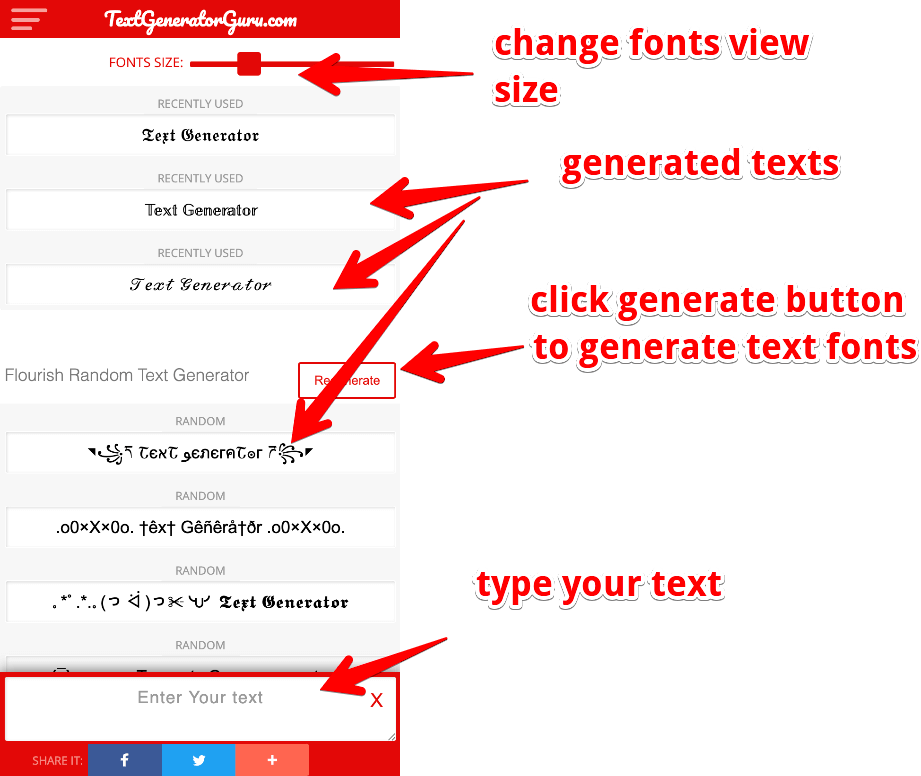
Which of Popular Text and Fonts, Text Generator Guru Can Generate?
Cool Text Generator
It converts any normal font to stylish fonts that look pretty cool. Cool text generator lets you copy and paste your desired font and use them in different online and offline platforms. Many people use them for fun or to attract followers on Instagram and other social networks. Cool text font looks like this: ℭ𝔬𝔬𝔩 𝔱𝔢𝔵𝔱 𝔤𝔢𝔫𝔢𝔯𝔞𝔱𝔬𝔯Small Text Generator
It converts big fonts to small fonts and helps you to shorten the space your font would take otherwise. You can get the small fonts by simply copy pasting a text on small text generator. Small text font looks like this: small text generatorWeird Text Generator
We all love weird fonts when it comes to playing with words. Weird text generator converts normal fonts to weird ones when you copy and paste a text. You can try it on social media and other platforms for fun. Weird text font looks like this: ῳɛıཞɖ ɬɛҳɬ ɠɛŋɛཞąɬơཞZalgo Text Generator
It converts a normal text into zalgo text when you copy and paste it on any online or offline platform. In zalgo text generator, the normal text grows taller and catches glitch with added text symbol and scratchy noise, which is a trendy way to decorate your social media bio. Zalgo text font looks like this: z̸̻̭̟̣̓͊̑̊ȧ̴̛̟͙͕̱̣̖̞͚͚͎̗̱͒̂̓͆̾͛̓̎͒̕ͅl̴̢̧̡͕̼̩̞͚̯̓̆͆̃̽̄̓̒̊̐͒͑̚͜ģ̷̢͔̠̺̣̺͕̞̖͕̱̫͔͎̐̂̐͑͛͗̿̒͋̉͋̎̈́̚o̸̗͕̩͇̼̙̲͔̺̻̝̖̣͛̐̇͂̔͆͛̈́̕̚̚̚̚͜ ̴̢͚̖̠̲́̇̓̑̅̃̍̌͑̄͒̾̌͘t̵̻̖̙͔͎͈̘͉̫̑̑͛͋̐͌͂͜͝è̴̥͓̬͑̀̋̄̑͋̍̃̚͘͝x̸̟͉̺̗̜̜͕̝̱̙͎̒̒͛͝t̷̛̤̹͔͍͍̪͉̘̘̻̋̿̽͝ ̸̺̝̼͚̺̲̙̹́̓͗g̴̭̮̪̣̘̩͎̮̟̩̹̲͔͗̿̋̈́͜ͅę̴̛̟͉̹͔̣͒̀̑̐͆ņ̵̛̦̝͎̮͗̏̌̈́̽̈́̕̕͝͝e̸̟̓̽̈́͆̿̈́̄͂͗͊̚͠͠ŗ̴͎̹̔̅̌͐́̓̔́͛͒̂͝͠a̴͈͙͛̀̿̀̆̄͆͗͒̾̾̈̔͝ẗ̵̗̭͇̹̣͚̗̗̭́͛͐͆̾̀̄̑̋̔͐͠ͅơ̶̘̯̳̪͓̇̍̐̋̓̄̊̇͝͝ŗ̸̩̳̗̂͆́͂̾̓̚͝Tiny Text Generator
It converts bigger fonts into tiny sized fonts that you can simply copy and paste to use. Usually, tiny font generator gives you multiple options in tiny font styles. You can explore the styles and choose the most attractive one depending upon your purpose. Tiny text font looks like this: ᴛɪɴʏ ᴛᴇxᴛ ɢᴇɴᴇʀᴀᴛᴏʀBold Text Generator
It converts normal fonts to bold fonts and gives you multiple options in bold font styles to pick. All you need to do is copy and paste the text from bold text generator. Many people use it to highlight some important points they want the readers to note. Bold text font looks like this: 𝐛𝐨𝐥𝐝 𝐭𝐞𝐱𝐭 𝐠𝐞𝐧𝐞𝐫𝐚𝐭𝐨𝐫Glitch Text Generator
It converts normal fonts to stylized glitch fonts and lets you use it in online and offline platforms by simply copy pasting the text you want. You can use flitch text generator to break the monotony of normal fonts in your post or bio profile on Facebook and Instagram. Glitch text font looks like this: ǧ̵̨̜̲̭̹̽́̉̍l̶̼̳͕̼̝͖̝͒͊́̒̇̓̈́̈́̑͌͌̌̓̾͝į̷̧̨̢̛͖̥̠̳̜͋͊͒̿̔̐͊̚ẗ̴̗̜̜͖̻̳̞͙̬͍̝̞̜̭́̌̚c̸̡̨̠̤͙̹̗͚̯̻̙͖̅̉͝ȟ̶͓͇͙̮͑͊͋̈̄̓́̕ ̴̡̣̦̦̪͍̗̗̆̍̓̐̿̅͝t̵̛̫͍̪̙͇̱̞̺̰̍̑͐̄͛͂̋̔͐̍e̴͙͉̰̠̮̾͠x̸̡̣͙̠͓̦̤͕̖̥͙̆̾̑͌̕t̸̨͙̯̩̠͚͛̾̾͗̚ ̴̹̺͓̗̺͔̙̺͖̮̠̒g̶̨̡̜̫̰̼̈́́̾͠͠ë̶͇̻̱̠̲̙́̓͒̈́͐̆͊͠͝n̴͔̞̪̦̙̪̟̥͖̎̓̓͆̓̓̈̐̾̉̍̇͆ę̷̰̬̰͉̓͂̉̏̔̓r̴̙̱̹͊̆͐͌̇̈̽̀͘͝ͅä̵͉̰̱̞̘́̑̿̇̑̆t̵̗̘̞͛̏̿̾̔͒̍̔̍͜ͅǫ̴̞̞̺̗̺̣̖͉̖̋͜r̵͍͓͖͓̲̭̪̼͉͈͉͂̃͌̿͜͜͠Upside Down Text Generator
It converts the style of a font by turning it upside down. Upside down text generator can add a lot of fun and twist to your normal boring text where people will actually make an effort to read this font. You can simply copy and paste the typed text to use the upside down font. Upside down text font looks like this: ɹoʇɐɹǝuǝƃ ʇxǝʇ uʍop ǝpᴉsdnCursive Text Generator
It helps you to stylize a font by automatically converting it into cursive font. The word cursive comes from curve and you get curvy stylized fonts from a cursive text generator. All of us are acquainted with script font and now you can use it on any platform you want. Cursive text font looks like this: 𝒸𝓊𝓇𝓈𝒾𝓋𝑒 𝓉𝑒𝓍𝓉 𝑔𝑒𝓃𝑒𝓇𝒶𝓉𝑜𝓇Creepy Text Generator
It converts normal font to creepy fonts that look extremely stylish. If you have a fetish for creepy stuffs, you can make the most of the creepy text generator to attract the readers. You can copy and paste the creepy text into chat messages, bio profile and other places. Creepy text font looks like this: 𝖈𝖗𝖊𝖊𝖕𝖞 𝖙𝖊𝖝𝖙 𝖌𝖊𝖓𝖊𝖗𝖆𝖙𝖔𝖗Vaporwave Text Generator
It lets you convert any normal text into vaporwave text by adding more space between wide letters. Vaporwave text generator can be used while writing captions or catch lines in your social media posts. Vaporwave text font looks like this: vaporwave░text░generatorBackwards Text Generator
This simple text generator converts normal text into backwards text by putting the letter orders in a complete reverse style. If you type a text on backwards text generator, the result will be just like mirror with letters in a reverse manner. Backwards text font looks like this: rotareneg txet sdrawkcabRandom Text Generator
This text generator converts the font style of any random text you type into fancy stylized fonts. Many people use it for fun as well as for serious work as they want to use aesthetic font. Random text generator has a wide variety of fonts.Random text font looks like this: ɾąղժօʍ էҽ×է ցҽղҽɾąէօɾ
Cursed Text Generator
This text generating tool can make your normal text look extremely stylish by converting its font into cursed style. Some cursed text generator also lets you play a lot with your words by increasing the crazy level of the text. Isn’t that fun?Cursed text font looks like this: c̷̣͉͚̝̘̹̥̬̥̞̙̈́̎̄͂̑̿̈́̚̚ͅṷ̶̢̧̡͔̻̠̣̺͚̻̪̤̝͙̄̊̍̎̑̂͆r̷̛̜͓͋̐̎͊͛͂̇́̄̃͊͘͠s̶̛̰̏́̅̉͆̾̀̆͛̿̑e̴̻͓̩̫͚̓̎͊̈́̓̂̓̐̿̚ͅd̶̗̤̥̩̤͖͔̃̎͜ ̷̢̛͈͙̱̻̭̗̰̿̐͋ͅţ̴͖̫̘̼͔̹̫̲͚̼̥̎̍͜ḝ̸͗̊͊̃͠x̶̳͇̌t̶̛͎͑̄͌̀̌̾ ̸̢̢͍̮͎̯̖̩͇̼̞̿͜͜͝ͅͅg̸̢̘̋ë̴̗͖̝͍̯̫͉̳̻̯́̐̓n̷̢̲̘͔͈͖͍͈̝͉̝͂̄̓̿͗̉̃̑̕e̷̡͍͎̘͙̟̫̱̅̉̏͛̓̆͑̿͒͊͑̚̚͠ͅr̴̨̘͉͖̲̭͎̞̪̼̒̂̔̉̒͌̄̈́̾̒̂̽̓̀͝a̵͉̘̤̖̫̲͕̟͈͂͋̔͌͐̈͗̔́͆́͝ţ̵̢̡̛͔͖̫̗͙͓͔͕̜͇̄̀̌̊̃̈́͜ö̵̡̢͉͉͓̞̃̐̂̔͗̎͑͗͠͠͠͠͠r̴̨̧̧̺̦̖̰̲̭̤͋̒̑͛̿̋̀͊̆̑̾̍̇͜
Glitchy Text Generator
What this simple font generator does is that it converts a normal text into glitchy text by changing its font style. It is a great way to attract followers in your social media profile. You can copy and paste the text from glitch text generator to use it.Glitchy text font looks like this: g͙̮̪̽̇͞l̦̠̺͇̎̅̽͊ȉ̳̦͍̺̏̃̾͟͞t̨͕̏̒c̙͊͐ͅh͖̼̲͒̎͡ỷ̨̙̪͉̓͂̓ ̺̘͈̀̽͡t͉͘e̘͗̈ͅx̠̝̫͖̌̇͑̒̕͢t ̤̃g͎̉ḛ̣̐̀n̲̙̳̍̂̽ē̼̓̚͟ͅr̛̥̭̩̬͊̾̆a̹͋ţ̛̫͙̭̒͑̍ỏ̞͙̣̑͂ṙ̲̰͉͋̿̋ͅ
Special Text Generator
Any normal text you type on a special text generator will be converted into a stylish text with a wide variety of fonts available for you to choose from. All you need to do is type or paste your text in it and choose your desired font by copy pasting it.Special text font looks like this: ֆքɛƈɨǟʟ ȶɛӼȶ ɢɛռɛʀǟȶօʀ
Stylish Text Generator
It generates normal text into a vast collection of stylish texts that you can easily choose and use by copy pasting. Stylish text generator presents a wide range of font styles and each font looks different. So, pick the best one according to your taste. Stylish text font looks like this: 𝔰𝔱𝔶𝔩𝔦𝔰𝔥 𝔱𝔢𝔵𝔱 𝔤𝔢𝔫𝔢𝔯𝔞𝔱𝔬𝔯Undertale Text Generator
You can turn your simple text into undertale text logo with a smart undertale text generator. It converts the normal fonts of any text into undertale text and allows you to copy and paste it for further use.Undertale text font looks like this: u̳n̳d̳e̳r̳t̳a̳l̳e̳ ̳t̳e̳x̳t̳ ̳g̳e̳n̳e̳r̳a̳t̳o̳r̳
Cool Fancy Text Generator
It converts a simple text into cool and fancy text by automatically changing its font. Cool fancy text generator has a wide variety of cool and fancy fonts that look amazing. You can copy and paste the most preferred text on any platform. Cool fancy text font like this: ₵ØØⱠ ₣₳₦₵Ɏ ₮ɆӾ₮ ₲Ɇ₦ɆⱤ₳₮ØⱤ3d Text Generator
Want to add some depth to your text? Well, 3d text generator converts the font style of a normal text into 3d font style. You can simply copy and paste the 3d text in online and offline platforms to use it.3d text font looks like this: 𝟛𝕕 𝕥𝕖𝕩𝕥 𝕘𝕖𝕟𝕖𝕣𝕒𝕥𝕠𝕣
Reverse Text Generator
What this simple text generator does is that it transforms a text into reverse order text. Reverse text generator is fun to use and it actually grabs a lot more attention to some special words you wish to highlight in a post.Reverse text font looks like this: rotareneg txet esrever.
Big Text Generator
It enhances the size of your normal text and turns it into bigger text. Also, big text generator gives you a variety of big font styles to choose from. You can simply copy and paste the desired font to use them on Facebook, Instagram or Twitter.Big text font looks like this: █▄▄ █ █▀▀ ▀█▀ █▀▀ ▀▄▀ ▀█▀ █▀▀ █▀▀ █▄░█ █▀▀ █▀█ ▄▀█ ▀█▀ █▀█ █▀█ █▄█ █ █▄█ ░█░ ██▄ █░█ ░█░ █▄█ ██▄ █░▀█ ██▄ █▀▄ █▀█ ░█░ █▄█ █▀▄
Strikethrough Text Generator
This fancy font generator automatically converts the font style of a given text into strikethrough styled font. This interesting font style is perfect for social media profile bio. So, if you are up for some unique trick to highlight your Insta bio, this one makes a great option.Strikethrough text font looks like this: ̶s̶t̶r̶i̶k̶e̶t̶h̶r̶o̶u̶g̶h̶ ̶t̶e̶x̶t̶ ̶g̶e̶n̶e̶r̶a̶t̶o̶r̶
Corrupted Text Generator
What this text generator tool does is that it changes the font style of any normal text into corrupted font style. You can further adjust the crazy level of the font style. Corrupted text generator makes anything you write look offbeat and striking.Corrupted text font looks like this: c̴̬̮̙̗̳̝̣̖̎̈̒̏̓̓̓ȏ̶̧̢̡͚͉̖̣̙̦͉̓͋̄́ṛ̶͔̹̭̝̯̳̺͚͓̖̥̹͐̏̓͋̓̀̆̂́̉̚ͅͅŗ̶̧̲͖͔̦̹̼̭̜͍̈̍̿̏̿͂̿̔͋̓̿u̵̦̒̊̈́̀̇̑̈́̏̓͌p̶̨̢̞̗̹̭̭͇͕͓͇͉̦̲̎͛̕ţ̸̧͈̮̯̠̣̃̅̂̉ͅȇ̷̡̳̜̩͕̜̲̫̫ͅd̴͓̈́͑̆͗̈́̿͂̕ ̷͍̠͈̖͉̰͕͚̹̍̉̕͠t̸̪̰̰͓͓̭̺͔͓̹̩̄̾͑́̃͂͒͆̊͊͐̌͘ȩ̸̛̛̻̺̙̝̼̹̩̜͚͓̂̋͑̍̅͠x̷̤̹̣̻̻͖̥͈̺̪̤̤͙̻͕̋̒̽͝͠t̷̡̨͖̹͕̮̮̫̩̺̥͙̱͇̊͊ ̶̨͖̜̯͉̲͓͙̥̰̥̌̎̔͊̂̐̀̃̉̆̕ǧ̴̡̹͎̗̗̻̻̏͜͠è̶̱̼͖̳̯̹͕̞͔͇̭͛ņ̸̻̘̱̱͔̣̯͕͇͙͓̜̦̽̅̅͋̀͑́̔̓̍̚ͅê̸̢͎͕͈͇̠̞̩͜͠r̸͚̞͕͔̺͆̏̄̅̈́a̸̻̲̯̻͔̱̼̟͍̜͂̃́͌̇̇̌̐͝͝ͅͅt̴̢̥̗̗̭̣̹͉̱̭͎̲̰͔̱̀̅́̿͝o̶̼͚̗̻̱̹͈͗͜ŗ̴̱̞̣̮̫̲̩͌͊́̊̀͑̔̎̂̈́̇̄̾͝
Curved Text Generator
You can simply change the style of your text by copy and pasting from a curved text generator tool. The curved text generator presents a variety of curved texts. You can wish to make a portion of your post or bio look interesting with this stylish font.Curved text font looks like this: 𝓬𝓾𝓻𝓿𝓮𝓭 𝓽𝓮𝔁𝓽 𝓰𝓮𝓷𝓮𝓻𝓪𝓽𝓸𝓻
Crazy Text Generator
It converts a normal text into quirky and crazy text by changing its font style. There are many crazy fonts available at the crazy text generator. If you love to flaunt the crazy part in you, this one can be a great option. The cool crazy fonts look like this: ςгคչץ ՇєאՇ ﻮєภєгคՇ๏гWide Text Fonts Generator
Wide text fonts generator converts a normal text into wide text by widening its width. Anything you type on this font generator will appear wider and therefore, many people prefer it as headlines and catch lines.Wide text fonts look like this: wide text generator
Upside Down Text - Flip Text Generator
If you are a lover of offbeat and quirky font, you will love the amazing upside down text generator or the flip text generator. Upside down text- flip text generator helps you to use this font in multiple platforms by simply copy and pasting. Upside down text- flip text font looks like this: ɹoʇɐɹǝuǝƃ ʇxǝʇ dᴉʅⅎ -ʇxǝʇ uʍop ǝpᴉsdՈSquares Fonts Generator
Square fonts look beautiful in all forms of writings, be it as a part of your profile bio or as a long post heading. Now, you can incorporate square fonts in all platforms with the help of squares fonts generator.Square text font looks like this: 🅂🅀🅄🄰🅁🄴🅂 🄵🄾🄽🅃🅂 🄶🄴🄽🄴🅁🄰🅃🄾🅁
Mirror Text Generator- Upside Down Text
You can play a lot with the words you type as there are online tools like mirror text generator- upside down text. What it does is that it converts your normal text into mirror text by turning the font style upside down. Mirror text generator- upside down textfont looks like this: ʇxǝʇ uʍop ǝpᴉsdn -ɹoʇɐɹǝuǝɓ ʇxǝʇ ɹoɹɹᴉW Strikethrough, Double Strike, Tilde and Slash Through Text Generator It is a text generator tool that helps you to play a lot of fun with the words you write. It converts normal font into strikethrough, doubl strike, tide and slash through stylish fonts. Strikethrough, Double Strike, Tilde and Slash Through
Text Fonts look like this: S̶t̶r̶i̶k̶e̶t̶h̶r̶o̶u̶g̶h̶ ̶T̶e̶x̶t̶ ̶G̶e̶n̶e̶r̶a̶t̶o̶r̶, ̷S̷l̷a̷s̷h̷ ̷T̷h̷r̷o̷u̷g̷h̷ ̷T̷e̷x̷t̷ ̷G̷e̷n̷e̷r̷a̷t̷o̷r̷
Undertale Text Box Generator
It converts your normal text font into Undertale inspired text font that looks quite interesting. All you need to do is simply copy and pasting the converted text from undertale text box generator.Undertale text box font looks like this: undertale text box generator
Twitter Text Generator
It converts any normal text into fancy text that you can use in Twitter. Twitter text generator gives you a plethora of Twitter fonts. Young people are looking for these stylish font generators to grab attention of their followers on Twitter. One of the stylized Twitter font looks like this: tຟittēr tēxt ງēຖērคt໐rDistorted Text Generator
It converts any normal text into fancy distorted text that looks simply awesome. Distorted font is one of the most creative fonts that you can use to express something. You can copy and paste fonts from distorted text generator.Distorted text font looks like this: ᕲᓰSᖶᓍᖇᖶᘿᕲ ᖶᘿ᙭ᖶ ᘜᘿᘉᘿᖇᗩᖶᓍᖇ
Custom Text Generator
It is a text generator tool that automatically converts a normal text into custom texts that you can simply copy and paste to use in multiple platforms. It is a great way of portraying your beautiful words or emotions on various platforms. Custom text font looks like this: ⓤรᵗ𝑜ᗰ Ŧⓔ𝐱Ⓣ ǤᵉήⒺŘ𝓪ⓣⓄя 💞🐯Scary Text Generator
It is a text generating tool that automatically converts your simple text into scary texts that you can use in multiple platforms by copy and pasting. Scary fonts have been one of the most searched fonts for decades. It is time you try it.Scary text font looks like this: §¢år¥ †êx† gêñêrå†ðr
Italic Text Generator
It is a text generating tool that lets you copy and paste italic text in different platforms. Italic text generator converts the font style of your text into special italic text making it look curvy. Though denoting titles and names were its main purpose, today people use italic font to highlight some specific words in a sentence or an entire sentence. Italic text font looks like this: 𝘪𝘵𝘢𝘭𝘪𝘤 𝘵𝘦𝘹𝘵 𝘨𝘦𝘯𝘦𝘳𝘢𝘵𝘰𝘳Crossed Out Text Generator
This text generator tool allows you to use crossed out text in different online and offline platforms. To try this one on any platform, all you need to do is copy and paste a typed text on the crossed out text generator. The crossed out text generator font looks like this: ̶c̶r̶o̶s̶s̶e̶d̶ ̶o̶u̶t̶ ̶t̶e̶x̶t̶ ̶g̶e̶n̶e̶r̶a̶t̶o̶r̶Font Text Generator
It converts your normal text into something very stylish and fancy. It is quite fun to use font text generator as all you need to do is copy and paste the desired text on any platform. Font text can be of multiple varieties that you can explore. A specific font text looks like this: f̤o̤n̤t̤ ̤t̤e̤x̤t̤ ̤g̤e̤n̤e̤r̤a̤t̤o̤r̤Bubble Text Generator
It is a text generator tool that lets you copy and paste stylized bubble text. Today, the youngsters like these font styles more than the normal boring ones and therefore, this one is trending on many social media platforms. Bubble text generator looks like this: ⓑⓤⓑⓑⓛⓔ ⓣⓔⓧⓣ ⓖⓔⓝⓔⓡⓐⓣⓞⓡGlitter Text Generator
With glitter text generator tool, you can easily use stylized glitter text in any online or offline platform. All you need to do is type the desired text in this tool and copy paste it anywhere you want. Glitter text font looks like this: ˜”*°•.˜”*°• glitter text generator •°*”˜.•°*”˜Old English Text Generator
With this text generator tool, you can use old English font in any online or offline platform of your choice. Old English text generator converts the simple text into classic old English fonts that you mostly find in religious scriptures. The old English text font looks like this: 𝔬𝔩𝔡 𝔢𝔫𝔤𝔩𝔦𝔰𝔥 𝔱𝔢𝔵𝔱 𝔤𝔢𝔫𝔢𝔯𝔞𝔱𝔬𝔯Curve Text Generator
This text generator tool allows you to use curved text in many platforms including your social media profile bio. All you need to do is copy and paste the curved text. There are many reasons why people choose curve text generator over the others and the main reason is visual treat.Curve text font looks like this: 𝒸𝓊𝓇𝓋𝑒 𝓉𝑒𝓍𝓉 𝑔𝑒𝓃𝑒𝓇𝒶𝓉𝑜𝓇
Gothic Text Generator
It is an interesting text generator tool that allows you to copy and paste stylized gothic text in multiple online and offline platforms like Facebook, Instagram and Twitter. Gothic texts generator has a collection of fonts that are extremely spooky and you can try them out.Gothic text font looks like this: 𝔤𝔬𝔱𝔥𝔦𝔠 𝔱𝔢𝔵𝔱 𝔤𝔢𝔫𝔢𝔯𝔞𝔱𝔬𝔯
Luni Bubbles Fonts Generator
it is a text generator that converts the normal text into bubbled text that looks quite interesting. You can copy and paste the bubbled text from the luni bubbles fonts generator to use them in various platforms.Luni bubbles fonts generator looks like this: ⓛⓤⓝⓘ ⓑⓤⓑⓑⓛⓔⓢ ⓕⓞⓝⓣⓢ ⓖⓔⓝⓔⓡⓐⓣⓞⓡ
Cute Text Generator
This text generator converts simple text into something really cute and fancy. You girls prefer this font the most when it comes to writing Instagram and Facebook profile bio. To try the cute text generator, all you need to do is copy and paste. Cute text generator looks like this: 🐤 ⋆ 𝒸𝓊𝓉𝑒 𝓉𝑒𝓍𝓉 𝑔𝑒𝓃𝑒𝓇𝒶𝓉❀ 🐿 ⋆ 🐤Decorative Text Generator
It is a text generator tool that allows you to use decorative text in any online or offline platform. Decorative text generator gives you plenty of options while choosing stylish fonts. For most of the users choosing this text generator, visually pleasing fonts are the fist choice.Decorative text font looks like this: 𝔻𝕖𝕔𝕠𝕣𝕒𝕥𝕚𝕧𝕖 𝕋𝕖𝕩𝕥 𝔾𝕖𝕟𝕖𝕣𝕒𝕥𝕠𝕣
Text Design Generator
It is a tool that lets you use your favorite stylish fonts in any online or offline platform of your choice. It gives you a plethora of collection of fonts that you can explore. Many people like text design generator for its extensive collection of stylish fonts. Text design font looks like this: ȶɛӼȶ ɖɛֆɨɢռ ɢɛռɛʀǟȶօʀFree Text Generator
You can choose the fancy text of your choice and use in multiple platforms with the amazing free text generator. The generator lets you copy and paste the stylish font of your desire for free. When you can choose your favorite font instantly and that too for free, nothing like it! Free text font looks like this: 𝐹𝓇𝑒𝑒 𝒯𝑒𝓍𝓉 𝒢𝑒𝓃𝑒𝓇𝒶𝓉𝑜𝓇Text Generator Fonts
You can get the stylized font of your desire among the text generator fonts. These fonts can be used in multiple platforms like Instagram, Twitter and Facebook by simply copy and pasting. The collection of fonts is huge in text generator fonts. Text generator font looks like this: 𝓽𝓮𝔁𝓽 𝓰𝓮𝓷𝓮𝓻𝓪𝓽𝓸𝓻 𝓯𝓸𝓷𝓽𝓼Wavy Text Generator
You can use stylized wavy text in all your social media accounts and other platforms with the help of wavy text generator, which is for free. Wavy fonts look extremely gorgeous when you use them to write an exclusive post. Wavy text font looks like this: 𝓌𝒶𝓋𝓎 𝓉𝑒𝓍𝓉 𝑔𝑒𝓃𝑒𝓇𝒶𝓉🍩𝓇Retrowave text generator
If you are a lover of the retro font, you will love the amazing retrowave text generator. It helps you to use retro font in multiple platforms by simply copy and pasting. Retro fonts look absolutely classy when you use them to write cool stuffs. Retrowave text font looks like this: 𝖗𝖊𝖙𝖗𝖔𝖜𝖆𝖛𝖊 𝖙𝖊𝖝𝖙 𝖌𝖊𝖓𝖊𝖗𝖆𝖙𝖔𝖗Scrolling Text Generator
You can create scrolling text for your website or blog with the help of scrolling text generator. The text generator tool converts a simple text into scrolling text and lets you use it instantly. Scrolling text font looks like this: 【scrolling text generator】Little Text Generator
It converts any simple text to little text by making its size smaller. There is a vast collection of little text generator that you can choose from. Since we all have love for little things in life, this font can be added anywhere we want a special attention. The little text font looks like this: ˡᶦᵗᵗˡᵉ ᵗᵉˣᵗ ᵍᵉⁿᵉʳᵃᵗᵒʳMedieval Text Generator
You can use medieval English font in different online and offline platforms with the help of the medieval text generator. It lets you copy and paste the text that looks like the medieval style of English writing, classy and stylish. Medieval text font looks like this: 𝖒𝖊𝖉𝖎𝖊𝖛𝖆𝖑 𝖙𝖊𝖝𝖙 𝖌𝖊𝖓𝖊𝖗𝖆𝖙𝖔𝖗Fancy Text Fonts for Twitter

The young generation has a fetish for stylish fonts as these add a lot of freshness to their profile. You must have come across many Twitter profiles that have the user name and description decorated with stylish fonts. You can also stay updated by trying them out yourself. Our site will help you to Generate Fancy Text Fonts for Twitter.
Fancy Text Fonts for Facebook (Stories, Comments and Bio)
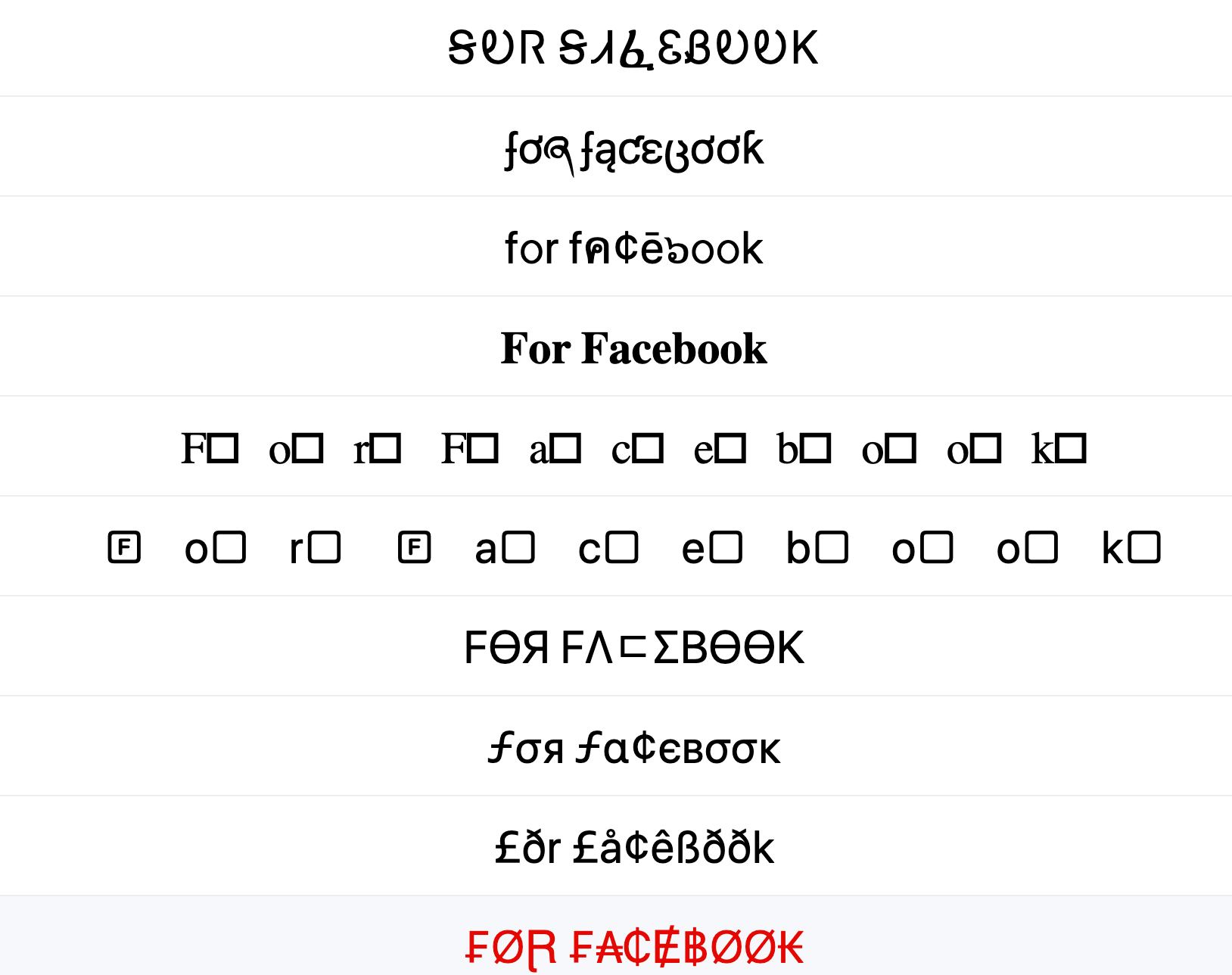
Many Facebook profiles and pages have these creative and stylish fonts and I would recommend you to try these. However, due to security reasons, not all fonts are supported by Facebook but most of these are. So, go ahead and try out. Textgeneratorguru will help you to Generate Fancy Text Fonts for Facebook (stories, Comments and Bio)
Fancy Text Fonts for Instagram (Stories, Captions, comments and Bio)

Using these fonts on Instagram is a great way of showing your creative side to friends and followers. Instagram allows fancy texts and therefore you can try them as your upcoming Insta stories, captions and bio. You can also comment on Instagram with these stylish fonts from my text generator tool. Create and Impress your friends with this unique Text Generator Tool which helps to generate Fancy Text Fonts for Instagram (Stories, captions, Comments and Bio)

